The Rocket Equation is a fundamental solution for rocket conceptual understanding and development. But did you know that there is an analytical solution to the distance, the integral of the rocket equation?

ΔV Solution

The ideal rocket equation links the change in velocity ΔV to the propulsion system’s effective exit velocity and the mass fraction. We often see these written in terms of the specific impulse Isp.

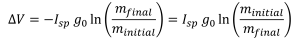
The critical conceptual points are that the velocity change depends linearly on Isp but non-linearly with the mass fraction. The trivial zero fuel case (i.e. final = initial) has a natural log of 1 which computes to a velocity of zero. As Gus Grissom says, “No bucks, no Buck Rogers.” Adding fuel increases the rocket’s velocity change, but only in a log proportion to the fuel added. The concept boils down to one concept: Accelerating fuel requires fuel.

The rocket equation is valid across the propulsion burn, such that the instantaneous ΔV is computed from the burn parameters. If we compute the final mass as:

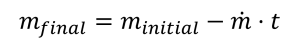
then ΔV(t) as a function of time is

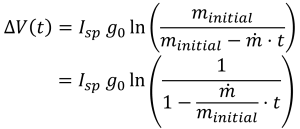
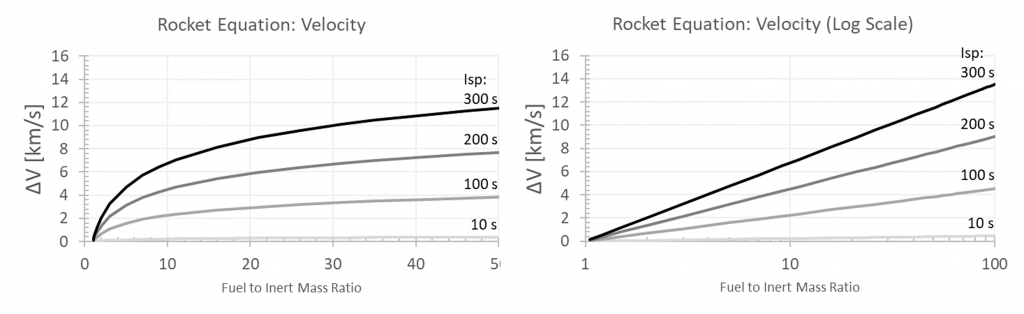
The second form consolidates the terms into two canonical parameters: (1) a propulsion term with Isp, and (2) a mass flow ratio to the initial mass. Implied in this form is the need to calculate the total burn time. The total burn time multiplied by the mass flow rate is the total propellant available, such that the final delta V is only a ln function of the ratio of propellant to initial mass and a linear function of the Isp. The following figure shows the delta V versus time for two different propellant mass flows.

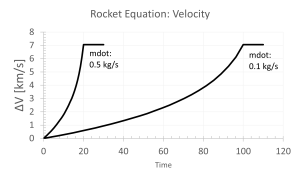
Integral Distance Solution

Now for the rest of the story. The integral of ΔV(t) is the rocket distance, which has an exact analytical solution. We will start with the canonical form from above.

Now, the rate of change of distance is velocity, such that the differential distance versus differential time relationship is:

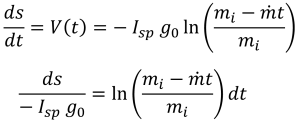
An analytical integral is available for this form, such that the distance traveled as a function of time when starting from rest in empty space is:

This can be particularly useful for verification of rocket solutions.

More to follow