How does surface roughness including frost and flaking paint affect aerodynamics? In this note, I take a look at the physics and the drag and stall characteristics of frost and flaking paint. A flight test of two Cessna 172s indicates the surprisingly large relative drag increment of flaking paint.
Author Archives: co
8s on Pylons
This engineering note discusses the commercial checkride 8s on pylons maneuver. The governing physics are used to derive the pivotal altitude and two strategies for adjusting the maneuver for lower powered aircraft.
Maneuvering Speed. Corner Velocity
In this engineering talk to the Texas Flying Club, I discussed maneuvering speed (aka corner velocity). This talk includes a discussion of the physics, applied calculations for the club’s Cessna 172 with a 2400 pound STC, references and discussions of the CAR 3 regulations governing most older aircraft, and a discussion of limitations of the regulations.

The important points to remember are:
- Maneuvering Speed only effectively protects against a SINGLE control input.
- Reduce Va at lower weights. A good rule of thumb is a reduction by half the weight ratio.
- Negative load limits and maneuvering speed are less than the positive load limits and Va.
Physics Club Talk
Pilot Rules of Thumb for Angles and Rates
This discussion of angles and rates for pilots will be presented at the Jan 2025 meeting of the Texas Flying Club.

Integral of the Rocket Equation
The Rocket Equation is a fundamental solution for rocket conceptual understanding and development. But did you know that there is an analytical solution to the distance, the integral of the rocket equation?
ΔV Solution
The ideal rocket equation links the change in velocity ΔV to the propulsion system’s effective exit velocity and the mass fraction. We often see these written in terms of the specific impulse Isp.
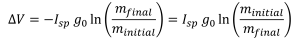
The critical conceptual points are that the velocity change depends linearly on Isp but non-linearly with the mass fraction. The trivial zero fuel case (i.e. final = initial) has a natural log of 1 which computes to a velocity of zero. As Gus Grissom says, “No bucks, no Buck Rogers.” Adding fuel increases the rocket’s velocity change, but only in a log proportion to the fuel added. The concept boils down to one concept: Accelerating fuel requires fuel.
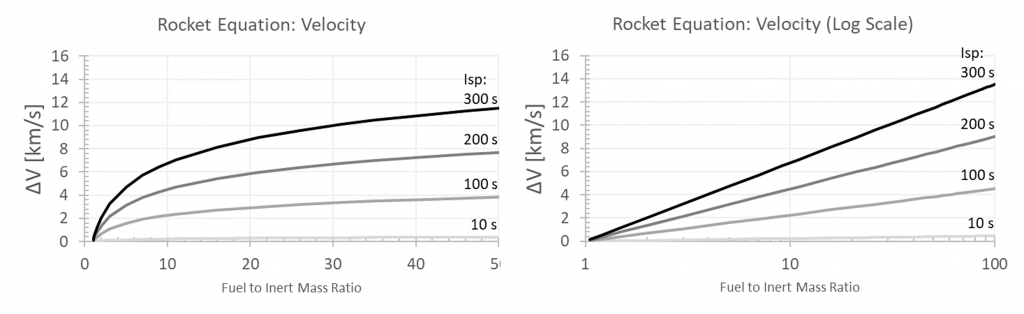
The rocket equation is valid across the propulsion burn, such that the instantaneous ΔV is computed from the burn parameters. If we compute the final mass as:
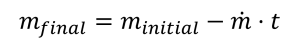
then ΔV(t) as a function of time is
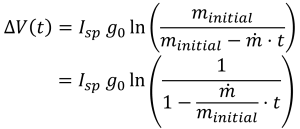
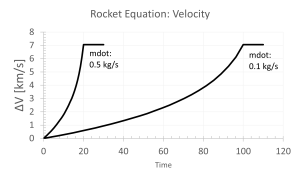
The second form consolidates the terms into two canonical parameters: (1) a propulsion term with Isp, and (2) a mass flow ratio to the initial mass. Implied in this form is the need to calculate the total burn time. The total burn time multiplied by the mass flow rate is the total propellant available, such that the final delta V is only a ln function of the ratio of propellant to initial mass and a linear function of the Isp. The following figure shows the delta V versus time for two different propellant mass flows.
Integral Distance Solution
Now for the rest of the story. The integral of ΔV(t) is the rocket distance, which has an exact analytical solution. We will start with the canonical form from above.

Now, the rate of change of distance is velocity, such that the differential distance versus differential time relationship is:
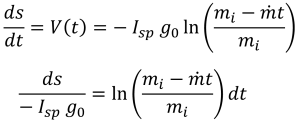
An analytical integral is available for this form, such that the distance traveled as a function of time when starting from rest in empty space is:

This can be particularly useful for verification of rocket solutions.
More to follow
Pathfinder Performance
These are the slides for the Texas Flying Club’s Pathfinder clinic.
Takeoff Performance Talk
I presented a takeoff performance talk at the Texas Flying Club. This discusses the theoretical and practical applications of takeoff performance.
Propeller Performance Talk
This is a talk for the Texas Flying Club.
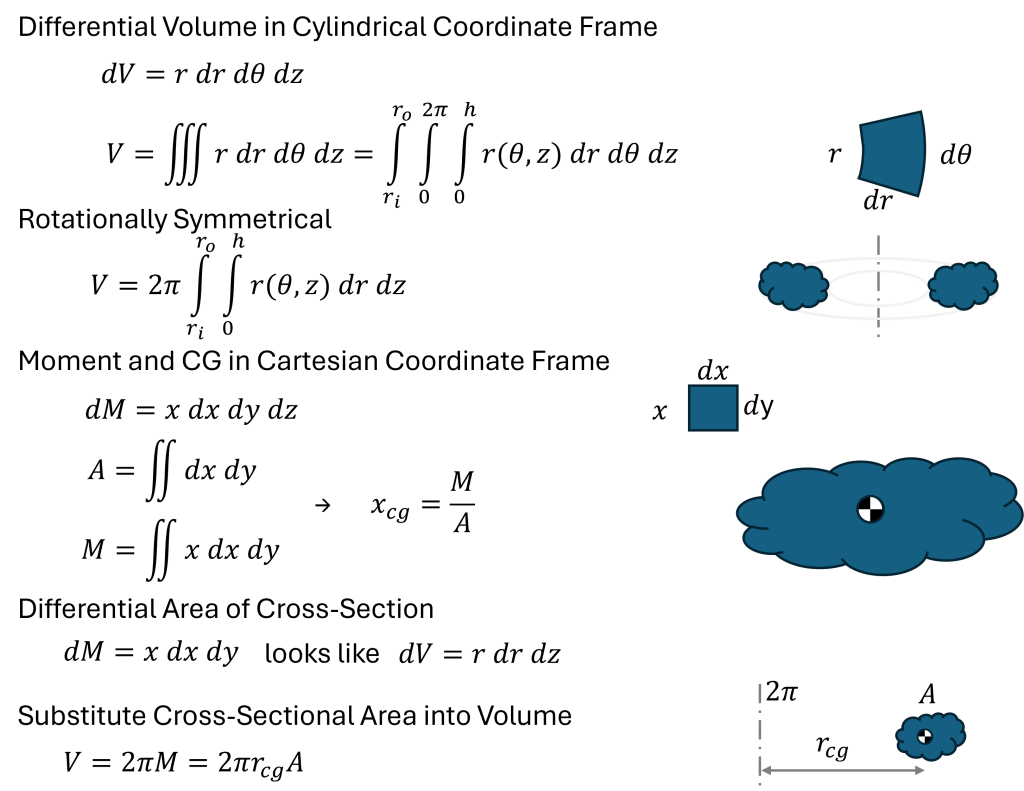
Rotationally Symmetrical Tank Volume
This note demonstrates how to quickly find the volume of a rotationally symmetrical enclosure. I find this approach useful for estimating and designing tank volumes. As an example, you can quickly find the volume of a toroidal tank with a 1 inch circle revolved about a line 2 inch from the circle’s center is slightly under 10 cubic inches (precisely π squared).

The equation is simple: Volume = 2π·A·L, where A is the area of the revolved cross section and L is the distance from the rotational axis to the center-of-gravity of the cross sectional area. For the torus, the area is 2π·πD2/4·L which simplifies to π2D2L/2. Neat and fast.
Here’s a design application: develop an equation for elliptical ended cylindrical tanks to hold precisely G gallons. Using the revolution equation in the figure below gives a total volume of V=πR2(h+4/3·b).
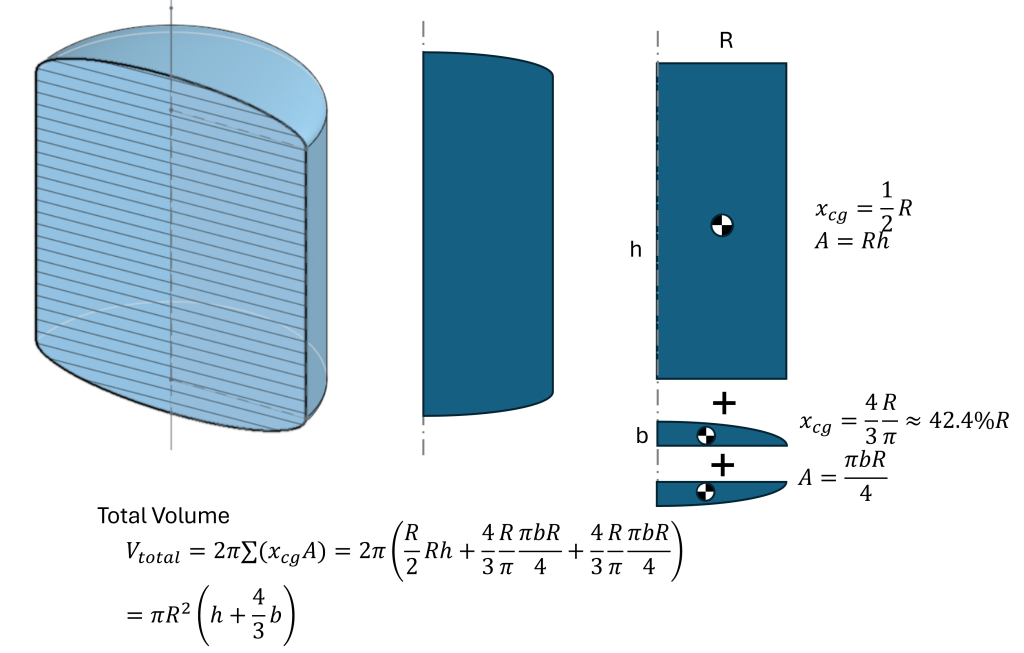
Now conversion to gallons is a linear transformation with 231 in3 per gallon.
This approach is also useful for crazy, bizarre, strange, and otherwise normal volumes of revolution. For instance, you can now find the volume of a specialty triangular o-ring seal.
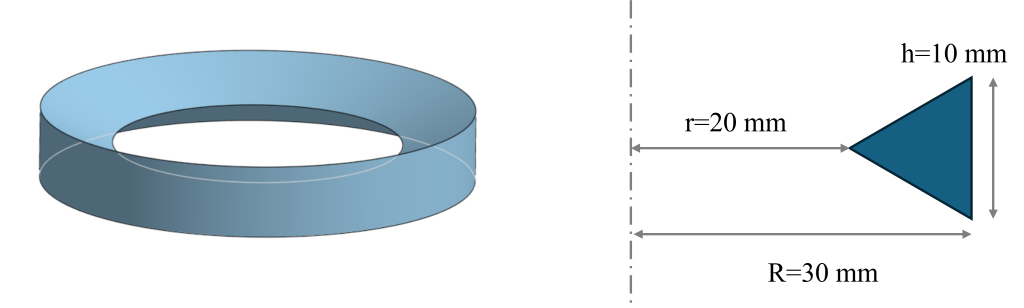
The triangular cross sectional area is half the base times height, so 50 mm2. The center of gravity of a triangle is 2/3 the way from the tip to the base, so that’s 6.6 mm. The total distance from the axis to the CG is 20+6.6 = 26.6 mm. Multiply and you obtain: Volume = 2π 50 * 26.6 = 8377 mm3
Why does this work?
The key trick here is recognizing that in cylindrical coordinates, the differential volume is dV=r·dr·dθ·dz, which appears to contain the moment equation dM=x·dx in a 2D Cartesian frame. A derivation is presented below.