This note demonstrates how to quickly find the volume of a rotationally symmetrical enclosure. I find this approach useful for estimating and designing tank volumes. As an example, you can quickly find the volume of a toroidal tank with a 1 inch circle revolved about a line 2 inch from the circle’s center is slightly under 10 cubic inches (precisely π squared).

The equation is simple: Volume = 2π·A·L, where A is the area of the revolved cross section and L is the distance from the rotational axis to the center-of-gravity of the cross sectional area. For the torus, the area is 2π·πD²/4·L which simplifies to π²D²L/2. Neat and fast.

Here’s a design application: develop an equation for elliptical ended cylindrical tanks to hold precisely G gallons. Using the revolution equation in the figure below gives a total volume of V=πR²(h+4/3·b).

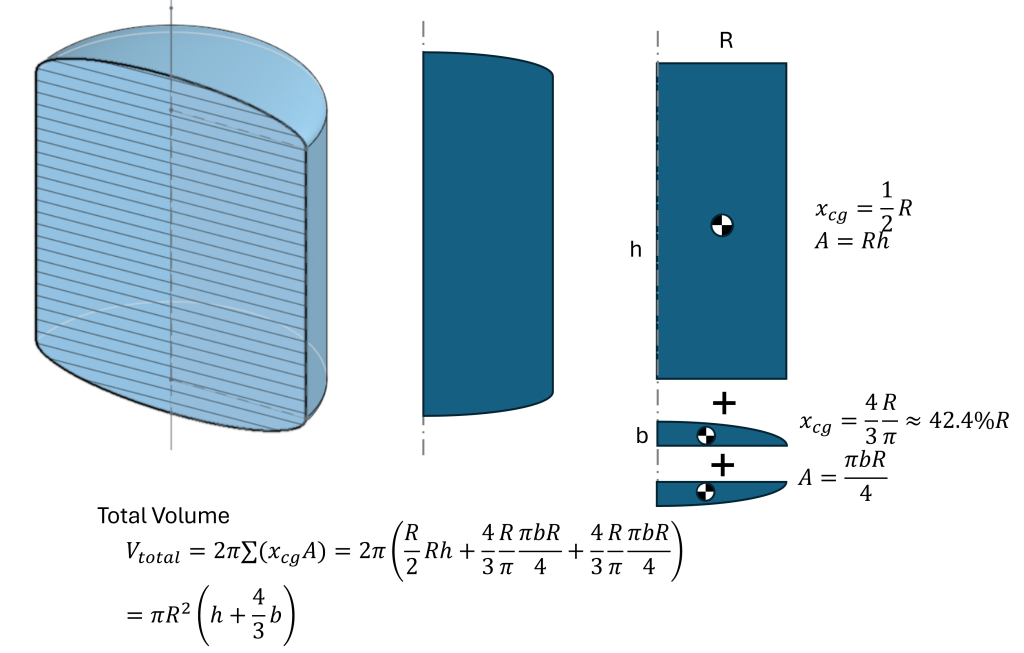
Now conversion to gallons is a linear transformation with 231 in³ per gallon.

This approach is also useful for crazy, bizarre, strange, and otherwise normal volumes of revolution. For instance, you can now find the volume of a specialty triangular o-ring seal.

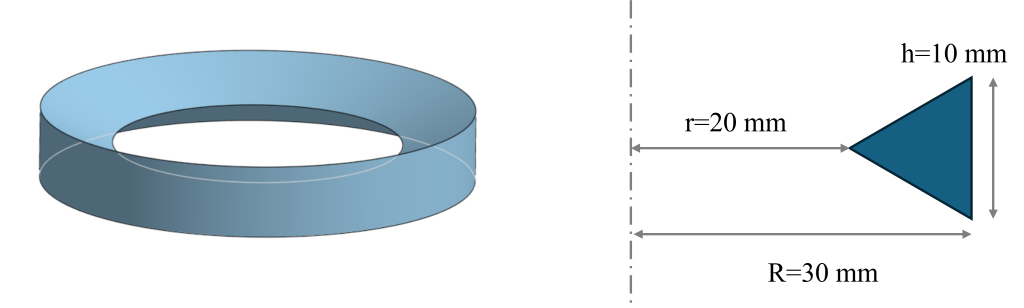
The triangular cross sectional area is half the base times height, so 50 mm². The center of gravity of a triangle is 2/3 the way from the tip to the base, so that’s 6.6 mm. The total distance from the axis to the CG is 20+6.6 = 26.6 mm. Multiply and you obtain: Volume = 2π 50 * 26.6 = 8377 mm³

Why does this work?

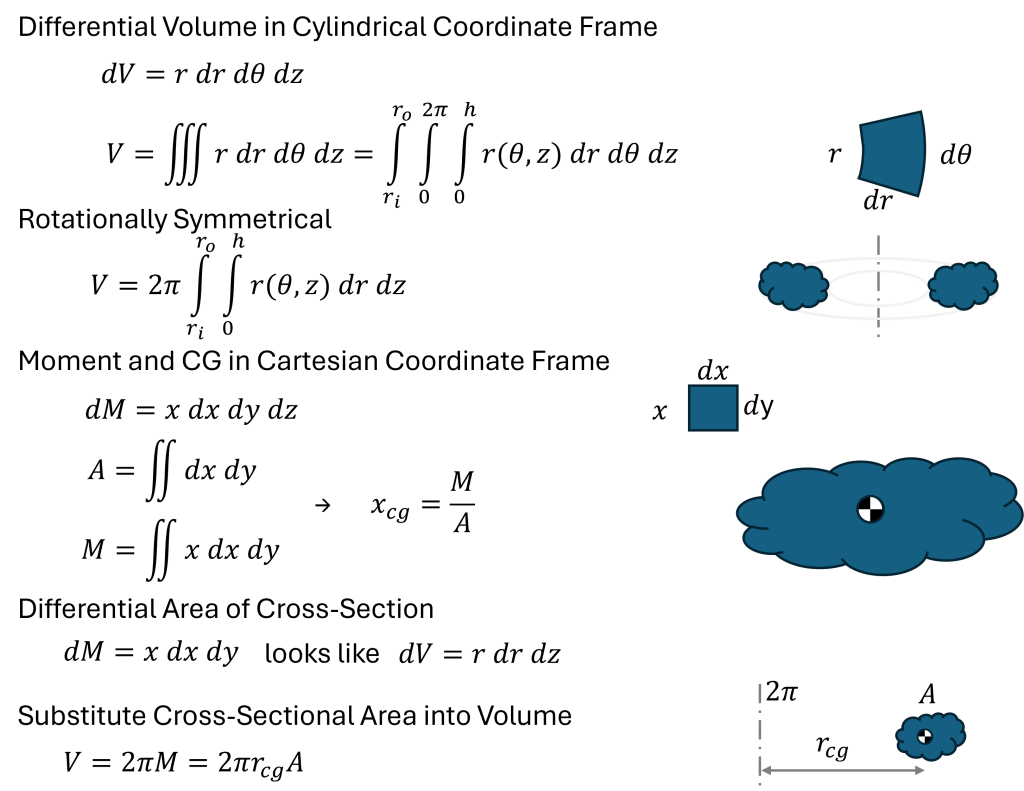
The key trick here is recognizing that in cylindrical coordinates, the differential volume is dV=r·dr·dθ·dz, which appears to contain the moment equation dM=x·dx in a 2D Cartesian frame. A derivation is presented below.