Prandtl Lifting Line theory remains an excellent tools for preliminary design and gaining intuition about the aerodynamics of unswept wings.

Implementing a PLL solver is relatively simple; I made this version in a few hours with Fortran. The solver generates SVG files displaying the wing geometry, gamma and lift distributions as well as the integrated lift and drag coefficients for arbitrary wing geometries (as approximated by linear sections). The program and input files are available at: https://charles-oneill.com/code/prandtl/prl2.zip

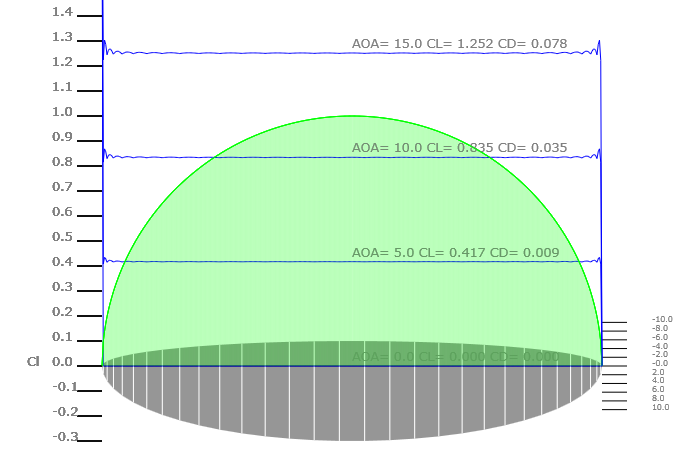
A flat elliptical wing demonstrates the flat sectional lift coefficient distribution resulting from an elliptical lift distribution.

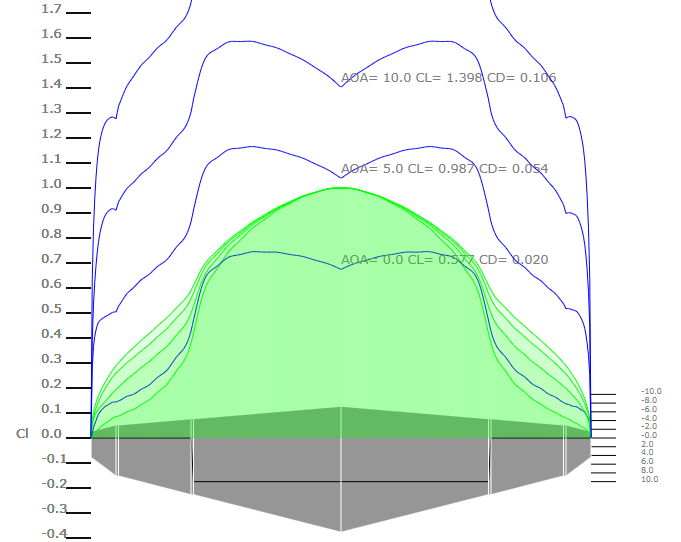
The beauty of the Prandtl lifting line theory is the ability to modify the wing geometry and airfoil sections. For example, given a 20% flap deflected 20 degrees on inner wing sections, the sectional lift distribution reflects the flap deflection. Of particular interest is that the shed vorticity is proportional to the slope of the green lift distribution.

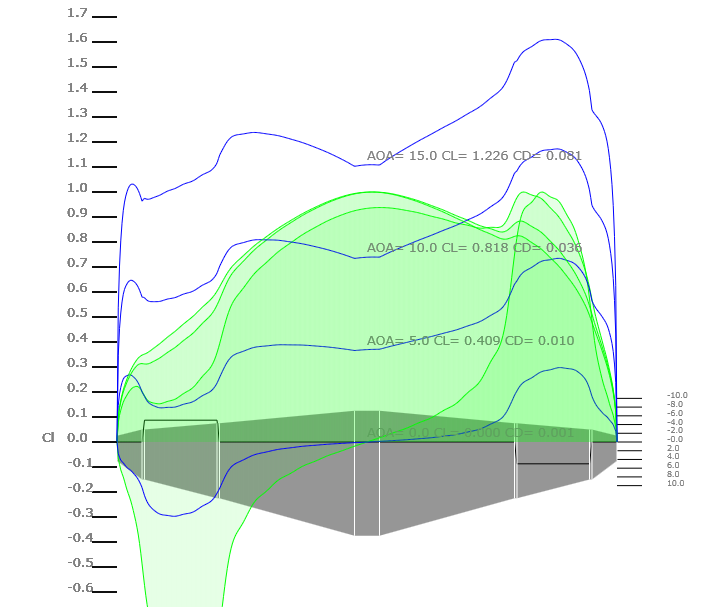
The PLL theory is also instructive for understanding control surface behaviors. In the following image, the 20% ailerons are deflected approximately +-10 degrees (Thin airfoil theory is used to determine the equivalent zero lift line.). Of particular concern is that aileron deflections at high AOA can push the local angle of attack into a stalled state.