Calculator:
Theory:
Warning: Don’t make this fundamental error in determining the density of moist air.
Recently, I’ve been preparing a graduate level course on Wing and Airfoil Theory. One lecture delves into modeling the real atmosphere including humid, wet, moist air. Specifically, I wanted to calculate the density of humid air. Visit my Atmosphere page for more information and tools.
[Update 1st March 2019] A moist air density calculator is at the top of this page.
My first thought was to grab a psychometric chart from my wife’s ASHRAE handbook which is available in pdf format at: ASHRAE Psychometric Chart No. 1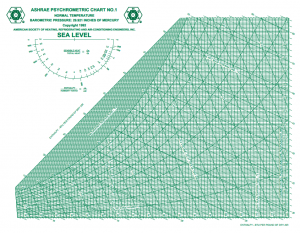
The chart plots lines of density, dry-bulb temperature, wet-bulb temperature, enthalpy, and relative humidity. As an example, at 90 F and 90% relative humidity, the chart indicates a volume per cubic foot of dry air of approximately 14.48. This gives a density of 0.00214 slugs per cubic foot.
However, this density is not the density of humid air. I didn’t catch the mistake until verifying my own independent calculating routine.
\(\) My derivation started with an ideal gas approximation of dry air and water vapor. The total pressure \(p\) is the summation of partial pressures for dry air \(p_d\) and water vapor \(p_w\).
$$\rho = \frac{p_d}{R_d T_d}+\frac{p_v}{R_v T_v}$$
Since the temperatures are identical, the density is:
$$\rho = \frac{p_d M_d + p_v M_v}{\bar R T}$$
Given that the relative humidity relates the partial pressure of water vapor to the saturation pressure of water pressure \(p_v = \phi p_s \), the density formula is rearranged to
$$\rho = \frac{p M_d + \phi p_s \left( M_v – M_d \right)}{\bar R T}$$
Since the molecular mass weight of dry air is \( 28.97 \frac{lbm}{lbmol} \) while water vapor is lower at \( 18.00 \frac{lbm}{lbmol} \), the density of wet air is always lower than dry air.
The reduction in magnitude depends on the saturation pressure of water vapor. For the region of interest to aerodynamics, the Arden-Buck equation provides a curve fit approximation to the partial pressure of water vapor. Converted to standard units, the partial pressure in psi given a temperature in R is:
$$p_s(T) = 0.08865 \exp\left(\frac{-0.002369 (T-8375.65)(T-491.67)}{T-28.818}\right)$$
Combining the density and partial pressure formulas gives an alternative estimate of the density of air at 90 F and 90% humidity of 0.002203 slugs per cubic foot.
So what gives? Who is correct? Why is the gold-standard ASHRAE chart suggesting a lower density? The key words are: volume per cubic foot of dry air. 
The ASHRAE chart gives the density of only the air and NOT the water vapor. The ASHRAE chart clearly states that only the dry air component is considered.
Adding in the water vapor requires finding the humidity ratio.
For the 90 F and 90% case, the humidity ratio is 0.028. Each 100 pounds of dry air has 2.8 pounds of water. Correcting the previous ASHRAE density gives:
$$ \rho = (1+0.028) 0.00214 \frac{slugs}{ft^3} $$ which is 0.002207 slugs per cubic foot.
Mystery solved.
Warning: There are websites out there inadvertently giving the wrong density of wet air. One example is denysschen.com. A single sentence would correct the confusion. On the other hand, the site at hvac-calculator.com appears to give the correct value.