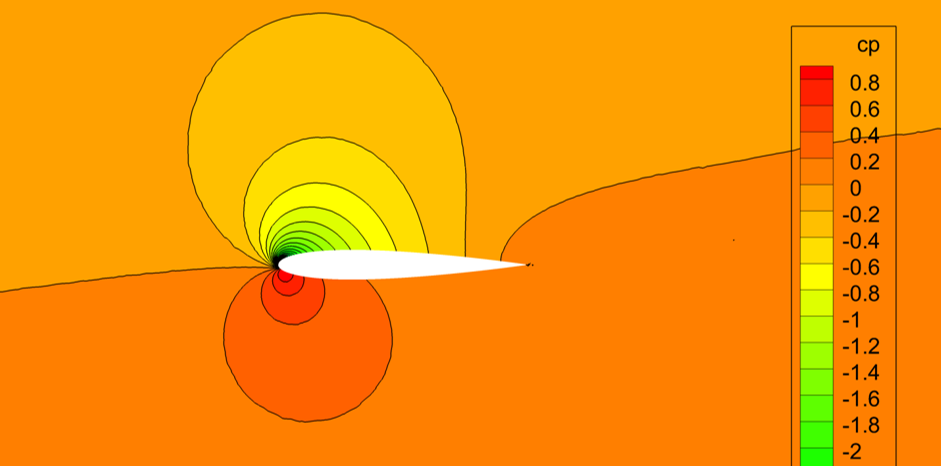
\(\)In the spring, a colleague asked a question regarding the computation of circulation about an airfoil. In response, I created a comparison of methods to calculate the circulation about an NACA 0012 airfoil at 10 degrees angle of attack, Mach 0.16 and a Reynolds number of 6 million. Data was generated with the FUN3D CFD solver with an SA turbulence model. The visualization is through TecPlot360. The pressure coefficient, \(C_p \), field is given below:

The definition of vorticity is: $$ \omega = \nabla\times V$$ In 2D, expanding gives $$\omega = \frac{dV_y}{dx} – \frac{dV_x}{dy} $$Computing the vorticity in the domain gives the following field.

Three methods will be used to determine the circulation \(\Gamma \) about the airfoil.

• Method 1: Compute from lift coefficient. The CFD solver estimates a lift coefficient of 1.09. From the Kutta-Joukowski theorem, lift per unit span is proportional to circulation. Solving for circulation gives $$ \Gamma = \frac{1}{2} V_o \rho C_l $$ Computing gives \(\Gamma = 1.04 \)
• Method 2: Integrate vorticity in domain. $$\Gamma = \int\int_A \omega dA $$ Computing gives \(\Gamma = 1.03 \)
• Method 3: Contour integral of velocity. A coarse numerical integral with 16 points manually sampled from the CFD computed velocity components \[\Gamma  =  – \oint\limits_S {V \cdot ds} \]. 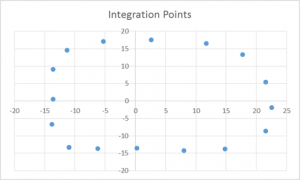This computation gives a circulation of \(\Gamma = 1.01\).