 |
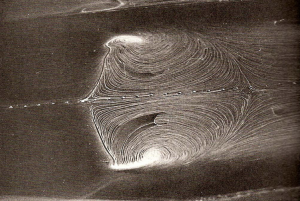
| J Green 1969 |
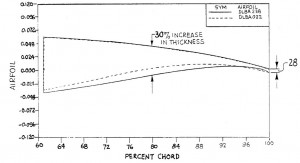
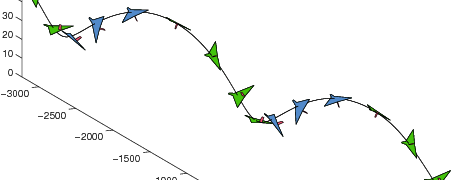
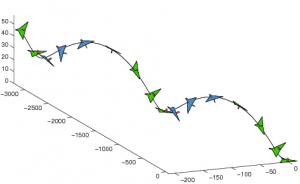
In the wind tunnel and production CFD environments, visualization of the fully 3D flow is a luxury rarely granted. For wind tunnels, even a 2D surface flow visualization is an expensive, messy, and incomplete tool. Learning to interpret and mentally visualize the flow structure is a critical skill.
So, in the spirit of a great book, SICP, the following documents from ONERA provide a wonderful explanation of the Structure and Interpretation of Surface Flows. After reading through these, you should be able to mentally visualize the 3D flow corresponding to the above image.