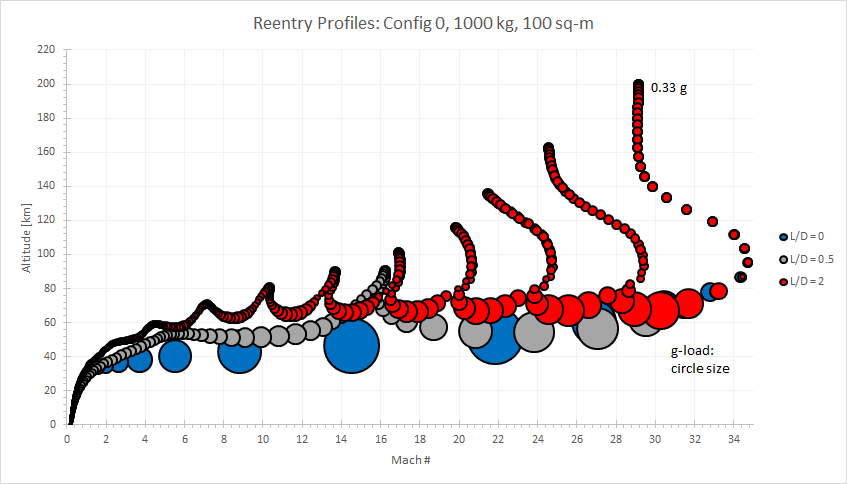
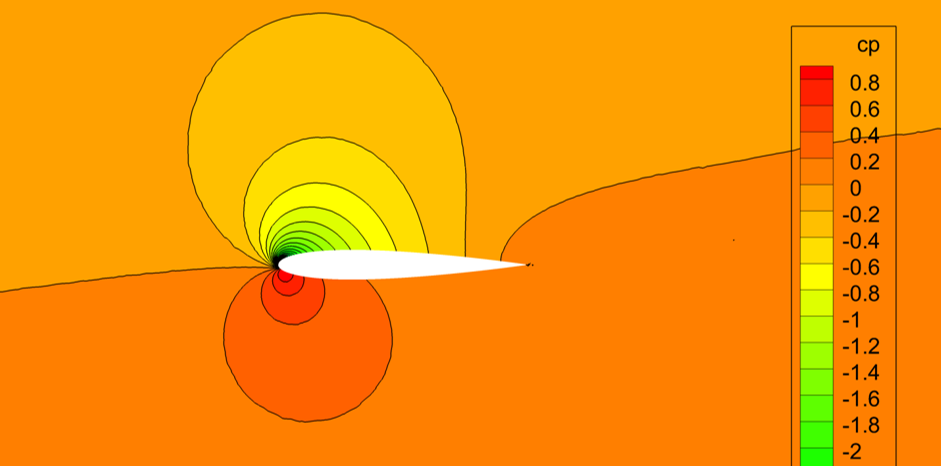
My students are strongly encouraged to demonstrate their capability through a web presence.
- Christopher D. Simpson (PhD student) http://www.cdsimpson.net/
- Chrisopher Ross Simpson (PhD student) https://simpsonaerospace.wordpress.com/
- Steve Pomroy (MS/PhD student) http://www.flightwriter.com/https://www.linkedin.com/in/stevepomroy
- Josh Richards (BSAE) https://www.youtube.com/watch?v=SWdLy5ZUDAM
- Easton Davis (BSAE) https://eastondavis.com/
- Daniel Stucki (BSAE) https://stuckidaniel.com/
- John Glidden (BSAE) https://john-glidden.com/