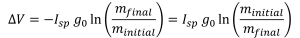Adding tip tanks to a PA-28 Cherokee or PA-28R Arrow?

I receive many questions about the fuel systems of Piper PA-28 Cherokees, Arrows, and PA-28-235 Pathfinders. A common question is:

How can I modify my PA-28 to add tip tanks from the PA-28-235?

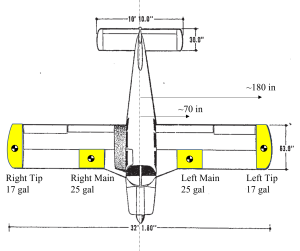
Thanks for the question. You have a good point, as the PA-28 Hershey bar wing chord is common across the PA-28R Arrow and PA-28 Cherokee variants prior to the tapered wing. Plus, the PA-28-235 and the Cherokee 6 have two 17 gallon tip tanks for a total of 84 gallons. 

Yet, for all of the advantages of these tip tanks, I’ve never seen or heard of them being retrofitted into a non-235 Cherokee or Arrow. I suspect that there are three primary reasons.

1) This modification is a major change and will require substantial engineering and flight testing work. I’m not aware of any STCs available.

2) The plumbing and fuel management systems are substantially different between the tip and non-tip PA-28 variants. Plus, the tip tanks significantly increase the fuel management decision making. The tips have capital and maintenance costs too.

3) The aircraft endurance/range performance in the stock aircraft is equal to or exceeds the normal endurance performance of the pilot and passengers. Additionally, adding 34 gallons of fuel effectively removes 1+ passenger, as you are unlikely to increase the certified gross weight for climb and structural performance reasons.

Given these negatives, how would I approach the installation of more fuel?

1) Sell the Arrow and buy a Bonanza.

2) Selling the Arrow and buying a Lance won’t work, as the larger engine burns substantially more fuel. I burned 9 gph in an Arrow and 14 in a 235. 

2) Add the PA-28-235 tip tanks but *don’t* copy the -235’s fuel system. Rather use a gravity or electrical pump into the existing fuel line, such that you one-way transfer fuel into the mostly empty main tanks. This has the potential to be an easier and safer certification path.

Now for the lawyer statements: 1) I am not advocating this process. Buy the Bonanza and be done with it. 2) I have not and will not indicate the legal, structural, or performance suitability of this process except under contract. 3) I am not presenting myself as a Designated Engineering Representative DER.

The answer really is no unless you have unlimited funds and time.

Aerodynamics Myths

This engineering talk discusses aerodynamics, lift generation, and a couple of common myths that persist in the aviation community. The talk was presented at the July meeting of the Texas Flying Club (http://www.texasflyingclub.com/). As a general guideline, the audience was comprised of pilots, such that the mathematics and physics are not presented as a formal proof but presented with the intent to convey understanding. One key point made is that any discussion of aerodynamics concepts must be consistent with continuity of mass, momentum, and energy. A simple freestream, source/sink, and vortex model was presented to explore a consistent understanding of aerodynamics for aviation.

AeroLiftMythsDownload

One Vortex to rule them all, One Vortex to find them,
One Vortex to bring them all and in the darkness bind them
In the Land of Aerodynamics where the Myths lie

8s on Pylons

This engineering note discusses the commercial checkride 8s on pylons maneuver. The governing physics are used to derive the pivotal altitude and two strategies for adjusting the maneuver for lower powered aircraft.

EightsOnPylonsDownload

Maneuvering Speed. Corner Velocity

In this engineering talk to the Texas Flying Club, I discussed maneuvering speed (aka corner velocity). This talk includes a discussion of the physics, applied calculations for the club’s Cessna 172 with a 2400 pound STC, references and discussions of the CAR 3 regulations governing most older aircraft, and a discussion of limitations of the regulations.

The important points to remember are:

  • Maneuvering Speed only effectively protects against a SINGLE control input.
  • Reduce Va at lower weights. A good rule of thumb is a reduction by half the weight ratio.
  • Negative load limits and maneuvering speed are less than the positive load limits and Va.
ManeuveringSpeedDownload

Integral of the Rocket Equation

The Rocket Equation is a fundamental solution for rocket conceptual understanding and development. But did you know that there is an analytical solution to the distance, the integral of the rocket equation?

ΔV Solution

The ideal rocket equation links the change in velocity ΔV to the propulsion system’s effective exit velocity and the mass fraction. We often see these written in terms of the specific impulse Isp.

The critical conceptual points are that the velocity change depends linearly on Isp but non-linearly with the mass fraction. The trivial zero fuel case (i.e. final = initial) has a natural log of 1 which computes to a velocity of zero. As Gus Grissom says, “No bucks, no Buck Rogers.” Adding fuel increases the rocket’s velocity change, but only in a log proportion to the fuel added. The concept boils down to one concept: Accelerating fuel requires fuel.

The rocket equation is valid across the propulsion burn, such that the instantaneous ΔV is computed from the burn parameters. If we compute the final mass as:

then ΔV(t) as a function of time is

The second form consolidates the terms into two canonical parameters: (1) a propulsion term with Isp, and (2) a mass flow ratio to the initial mass. Implied in this form is the need to calculate the total burn time. The total burn time multiplied by the mass flow rate is the total propellant available, such that the final delta V is only a ln function of the ratio of propellant to initial mass and a linear function of the Isp. The following figure shows the delta V versus time for two different propellant mass flows.

Integral Distance Solution

Now for the rest of the story. The integral of ΔV(t) is the rocket distance, which has an exact analytical solution. We will start with the canonical form from above.

Now, the rate of change of distance is velocity, such that the differential distance versus differential time relationship is:

An analytical integral is available for this form, such that the distance traveled as a function of time when starting from rest in empty space is:

This can be particularly useful for verification of rocket solutions.

More to follow